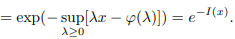Démonstration de la borne de Chernoff :
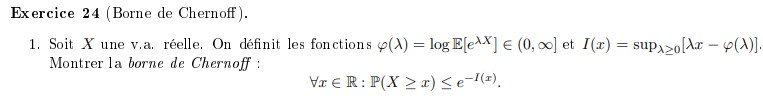
Utiliser que \(x\mapsto e^{\lambda x}\) est strictement croissante pour appliquer l'Inégalité de Markov.
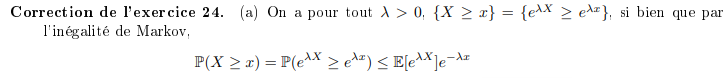
Réécrire en mettant tout dans la même exponentielle pour faire apparaître l'expression de \(I(x)\).
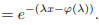
On peut passer à l'\(\inf\) sur \(\lambda\).
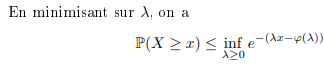
On retrouve l'expression voulue par décroissance, en passant le \(\sup\) en haut pour retrouver \(I(x)\).